26考研数学真题点评(数一点评)
- 2026-02-04 05:32:21
❝慎终如始,则无败事
昨天更新了26真题点评的整体点评部分,今天我们来写数一的点评。
❝点评之前,先插播一则启事,咱们的新年祝福活动,还有3名中奖同学没有联系我们,如果需要奖品的话,请尽快联系小助手(vx:yfli-mstudio~)哦~~
数一点评
今年的整体难度不高,选择题的难度大于填空题的难度,解答题在思考上的难度也不大,如果基础够扎实和计算够稳,得分应该也不难。选择题中,在概念上可能略有难度的是第2题、第3题与第9题,但前两道题选出正确答案的难度实际上没那么高。
1/5/6/7/8都属于相对比较容易的题,第10题的思考量不大,但比起其他题目而言,计算起来是比较繁琐一点。但其实,往年真题中,这种计算难度的题也不少。
填空题都是比较基础的计算题,没有什么技巧,计算难度也不大。
相比于其他年份,高数解答题中的证明题是比较常规的,比起22年和25年的压轴题,难度大大下降,比23年和24年的也显得稍微简单些。其余3道高数题,除了18题以外,也都是比较常规的,也就是说,如果我们按照目标80-100分去复习的话,有至少2道大题“应该”可以拿到满分。
个人感觉,虽然考了一个相对比较新的求矩阵的幂的方法,但今年的线代解答题比去年的数一线代解答题更简单一些。
概率解答题在整体点评过里已经分析过,就不再重复了。
下面逐题分析一下。



选择题
第1题
简单题,主要考查偏导数的计算。数二、数三也考了这道题。
第2题
概念题,是一道考法较新的题目。以前的考题基本上是利用比值法或者根值法来直接计算收敛半径,或者有利用阿贝尔定理来估计收敛半径的。
这道题的解法,见下面这篇推送,我们用了阿贝尔定理与级数收敛的必要条件。
第3题
概念题,主要考查对单调性与凹凸性的理解。错误选项较容易排除,但对凹凸性的考查,如果要正面证明正确结论,可能就不是那么容易。数二也考了这道题。
具体解法,见下面这篇推送,我们用到了同济教材上没有写的凹凸性的等价定义。
第4题
基础题,主要考查三重积分的计算中,如何利用柱面坐标系或球面坐标系将三重积分转化成三次积分,属于基础班就应该学会的知识。
它的图形,在1989年数一真题中,也出现过,虽然不是一模一样,但也可以说是如出一辙。

第5题
概念题,给出了置换矩阵这一新定义,主要考查对矩阵运算的理解。数二也考了这道题。
第6题
概念题,主要考查对向量组之间的线性表示与方程组有解之间的关系,关键条件是的列向量组可由的列向量组线性表示。
在2020年数一真题中,有一道也比较简单的有着类似条件的题。这两道题其实也有异曲同工之处。
若矩阵经初等列变换化成,则( )
(A)存在矩阵,使得.
(B)存在矩阵,使得.
(C)存在矩阵,使得.
(D)方程组与同解.
第7题
概念题,主要考查二次型与二次曲面之间的关系。
第8题
简单计算题,主要考查对的计算公式的运用。
第9题
概念题,综合考查了分布函数与概率密度的概念以及数学期望、方差的性质。
已知与的分布函数,由分布函数的定义可以得到与的关系,即与同分布,由此可以确定,.
或者,可以由与的分布函数得到它们的概率密度,再由的数学期望的计算公式可得到 与 的数学期望、方差之间的关系,再由此确定,.
第10题
计算题,计算量可能是10道选择题中最大的,当然,如果是在前几年真题中,就属于相对来说中等的一档。数三也考了这道题。
题目难度不大,就是按部就班地根据已知分布律以及条件概率来计算所需概率,计算过程相对来说是比较机械无聊的。
填空题
第11题
计算题,考到了向量积(这个概念很少考,但数一同学应该并不陌生)和散度。
在1995年数一真题中,有一道单独考查向量运算的题。
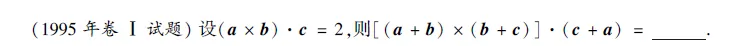
第12题
计算题,基础的型未定式求极限。数二也考了这道题。
第13题
计算题,求由参数方程确定的函数的二阶导数,二阶导数的表达式并不简单,但代值的话并不复杂。
第14题
计算题,分部积分与反常积分的组合。
这个积分在2000年数二真题中出现过。

第15题
计算题,主要考查特征值的计算。
第16题
计算题,主要考查数字特征的计算。数三也考了这道题。
解答题
第17题
计算题,常规的无条件极值计算,利用二元函数极值存在的充分条件判断即可。数二、数三也考了这道题。
第18题
综合题,综合考查了偏导数的性质与计算,以及微分方程求解。
第(1)问要证明,为常数,等价于证明,即. 注意到具有3阶连续导数,故具有2阶连续偏导数,从而,由此可以导出所证等式.
由第(1)问的结论可以得到一个关于的二阶常系数非齐次线性微分方程,从而结合第(2)问的条件可以求出的表达式.
这道题的具体解析,见下面的推送。
第19题
计算题,主要考查利用补线法与格林公式计算第二类曲线积分。
这道题与以往的补线不同的是,以往的补线,由题目设计,更多的是补沿着坐标轴的直线,而这道题里,连接曲线弧段的两个点的直线恰好通过椭圆的对称中心,这条直线将椭圆分成面积相等的两部分。于是,可以直接补这一条直线,与已知曲线弧段围成一个封闭区域。
第20题
证明题,比较常规的一道题目,综合考查了函数的性质与定积分的性质以及微分中值定理。
第(1)问可以使用中值定理(拉格朗日中值定理或加强版积分中值定理),再结合单调性得到,或者也可以将拆分成,利用换元将积分区间都变成后,再利用单调性得到.
第(2)问可以考虑对找到三个点,使得这三点处的函数值相等,从而使用两次罗尔定理得到存在,使得.
第21题
综合题,综合考查了极大线性无关组,向量组之间的线性表示与矩阵的幂。数二、数三也考了这道题。
第(1)问可以证明,线性无关且能表示,,,中的任一向量。
第(2)问实际上是要找出的列向量用其列向量组的极大线性无关组,的线性表示.根据, 的列向量即线性表示的系数。
这道题与2025年数三的线代大题关系非常密切,我们在下面这篇推文中写得比较详细。具体解析也可以看这篇推文。
26真题分享:向量组之间的线性表示与矩阵的幂(26数一第21题)
第22题
综合题,并且具有应用背景,综合考查了随机变量的函数的分布,无偏估计与最大似然估计。数三也考了这道题。
第(1)问中,分别记第个元件的寿命为,若试验出现1个元件失效即停止,则失效元件的寿命,从而是个独立同分布的随机变量的函数,由此可以求的概率密度. 求得的概率密度后,可以进一步求,从而确定的值以及计算。
第(2)问中,似然函数已给出,直接求该函数的最大值点即可得的最大似然估计值。
第(2)问中涉及到了基于截尾样本的最大似然估计,虽然解题本身并不需要这方面的知识,但是有可能对大家理解这道题带来一点困难。所以我们把浙大版《概率论与数理统计》(第四版)中关于这个知识点的内容放在下面。


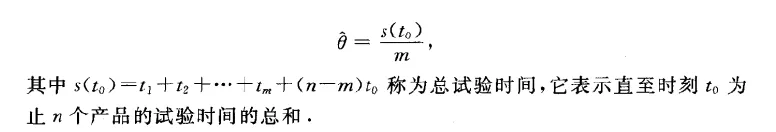
❝数一点评到此完毕~
感谢大家读到最后,在逐题的回顾过程中,我们会发现,往年真题的含金量真的是很高,实际上,在回顾完去年真题时,我同样也写过这样的感慨。希望大家在复习时,一定要重视真题,好好做真题~
27考研数学课程
课程咨询请加vx:yfli-mstudio.

全程班
基础班&


购课可点击文末“阅读原文”~前30名购买的同学可获得签名版教材~~~
高数指定教材

基础班高数指定教材
这套书知识点全面,讲解详细,非常适合自学。不购课的同学也可以自行购买这套图书自学高数内容。
购书推荐店铺:xhs@世纪高教版~
推荐店铺




