前面我们已经详细讲解了“二重积分罗盘包”的构建过程及如何应用,(相关内容可在“考点罗盘”合集中查看《二重积分疯了?坐标系选不对、定限乱,这个“罗盘” 救大命!》和《二重积分实战不用死磕!这个罗盘把“选系 - 定限 - 计算” 捋顺了》)。今天,我将带领同学们在真题中来实践罗盘包的使用过程。

确定是二重积分的题目时:调用二重积分罗盘包
模型调用
在这个模块中,我们将选用真题作为主战场,按照“罗盘包调用系统”精准解题
设平面区域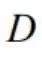 由直线
由直线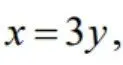
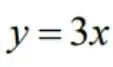 及
及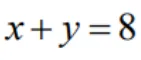 围成,计算
围成,计算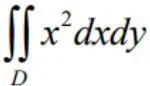 .
.
①筛选包:题目显然为二重积分的计算题目,筛选出二重积分罗盘包。
②匹配包:由被积函数不含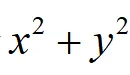 ,
,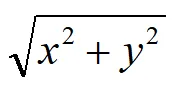 ,且积分区域
,且积分区域 与圆域
与圆域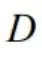
无关,则选择直角坐标系下计算二重积分,匹配出初始路径。
③检索包:匹配出直角坐标系下计算二重积分,检索其方法,画区域草图,确定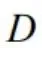 无可用的对称性,确定
无可用的对称性,确定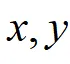 的上下限,化为2次定积分。
的上下限,化为2次定积分。
④碰撞包:无需碰撞。
第二步:书写证明过程
设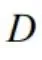 是由连线
是由连线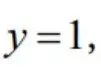
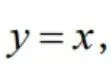
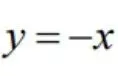 围成的有界区域,计算二重积分
围成的有界区域,计算二重积分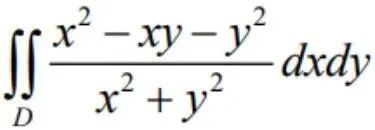 .
.
第一步:罗盘包调用过程,可以写在草稿纸上
①筛选包:题目为二重积分的计算题目,筛选出二重积分罗盘包。
②匹配包:由被积函数含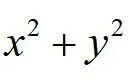 ,初步选择极坐标系下计算二重积分,匹配出初始路径。
,初步选择极坐标系下计算二重积分,匹配出初始路径。
③检索包:匹配出极坐标下计算二重积分,检索其方法,画区域 草图,且得
草图,且得 关于
关于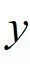 轴对称,又
轴对称,又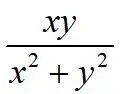 关于
关于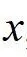 为奇函数,得
为奇函数,得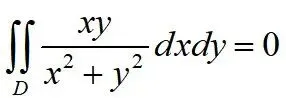 ,且
,且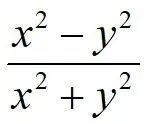 关于为偶函数,则
关于为偶函数,则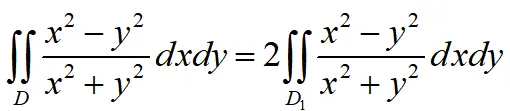 ,其中
,其中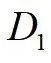 为
为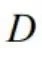 在第一象限内部分,确定
在第一象限内部分,确定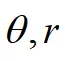 的上下限,化为2次定积分。
的上下限,化为2次定积分。
④碰撞包:无需碰撞。
计算二重积分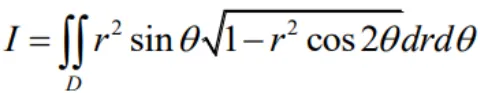 ,其中
,其中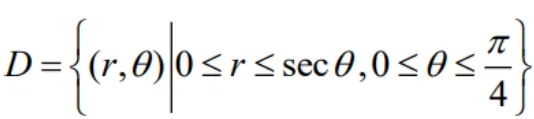 .
.第一步:罗盘包调用过程,可以写在草稿纸上
①筛选包:题目为二重积分的计算题目,筛选出二重积分罗盘包。
②匹配包:题目中为极坐标形式,但不易积分,则转化为直角坐标下计算二重积分,匹配出初试路径。
③检索包:匹配出直角坐标系下计算二重积分,检索其方法,画区域 草图,确定
草图,确定 无对称性,对
无对称性,对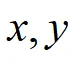 定限,化为2次定积分。
定限,化为2次定积分。
④碰撞包:无需碰撞。
第二步:书写证明过程
设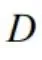 第一象限中的曲线
第一象限中的曲线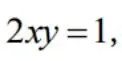
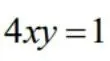 与直线
与直线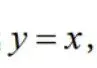
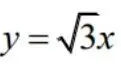 围成的平面区域,函数
围成的平面区域,函数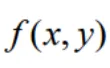 在
在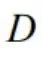 上连续,则
上连续,则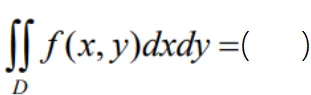
第一步:罗盘包调用过程,可以写在草稿纸上
①筛选包:题目为二重积分的计算题目,筛选出二重积分罗盘包。
②匹配包:题设中给定区域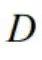 ,选项为极坐标系下化为2次定积分,则匹配极坐标下计算二重积分,匹配出初试路径。
,选项为极坐标系下化为2次定积分,则匹配极坐标下计算二重积分,匹配出初试路径。
③检索包:匹配出极坐标系下计算二重积分,本题只需要画区域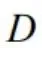 草图,定
草图,定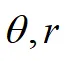 上下限,化为2次定积分即可。
上下限,化为2次定积分即可。
“各位奋斗在考研一线的同学们,通过“罗盘包”系统解决二重积分,我们不仅学会了一套工具,更掌握了一种高效的数学解题思维体系,面对题目是,能够有章法、有层次地进行拆解与判断。考研数学不是知识的堆砌,而是思维方法的较量。
通过本文的详细讲解,我们可以看到,二重积分罗盘包通过阶梯方法的策略整合,让同学们解题时快速定位方法,减少失误。
本文通过调用“二重积分罗盘包”这一高效工具,系统展示了如何快速选择坐标系、匹配对应方法并完成计算。罗盘包不仅涵盖了直角坐标系下和极坐标系下二重积分计算的通用方法,还包含直角坐标系下交换积分次序,此外,还罗列了坐标系下对应变量的定限方法。它不仅是解题的“导航仪”,更是理解与掌握积分技巧的“加速器”。
我的任务完成了,接下来的战场,属于你们!加油!”
思考题:
你可以评论区提问:调用二重积分罗盘包解决你所想解决的真题,我将具体给你写出解题过程
关注本公众号,不错过更新!
敬请期待下一个考点罗盘包吧
你还可以,转发给需要的人
1.给学数学没有头绪的人
2.给想挑战数学的人
3.给还在犹豫要不要学数学的人